Ok try to think about this, a person A gives something to person B and in return person B gives something in return, let's see this through a table.
Problem 1.
| Person A | Person B |
|---|---|
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
| 4 | 11 |
| 5 | 13 |
| 6 | 15 |
So how much a person B will give when person A gives 7?
Let's plot this exercise in a cartesian plane.
René Descartes was a French man who lived in the 1600s. When he was a child, he was often sick, so the teachers at his boarding school let him stay in bed until noon. He went on staying in bed until noon for almost all his life. While in bed, Descartes thought about math and philosophy.
One day, Descartes noticed a fly crawling around on the ceiling. He watched the fly for a long time. He wanted to know how to tell someone else where the fly was. Finally he realised that he could describe the position of the fly by its distance from the walls of the room. When he got out of bed, Descartes wrote down what he had discovered. Then he tried describing the positions of points, the same way he described the position of the fly. Descartes had invented the coordinate plane! In fact, the coordinate plane is sometimes called the Cartesian plane, in his honor.
Rene Descartes (Pronounced “day CART”) used the ceiling's axis to spot the fly.

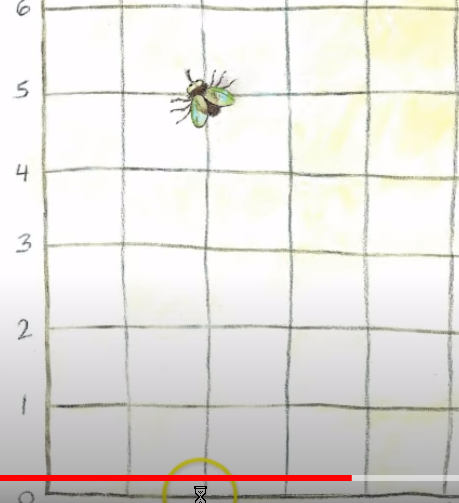
Fly is at (2,5)




Rene was a great philosopher but was also untidy and forgetful about his stuff in his house, so he marked them as same as he did with the fly.
ok coming back to our main problem, that is not a very easy one to understand so we will start with something easy.
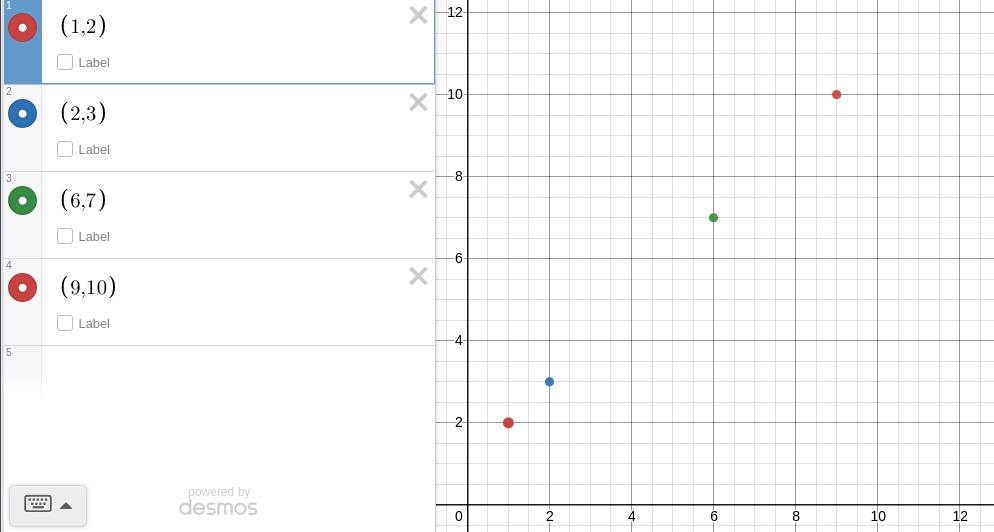
If you give me 1$, i will give you 2 candies 🍬 🍬
If 2$, 3 candies 🍬 🍬 🍬
If 6$, 7 candies 🍬 🍬 🍬 🍬 🍬 🍬 🍬
If 9$, 10 candies 🍬 🍬 🍬 🍬 🍬 🍬 🍬 🍬 🍬 🍬
So how can we plot this on a cartesian plane, we will do the same as Rene did with the fly on the wall.
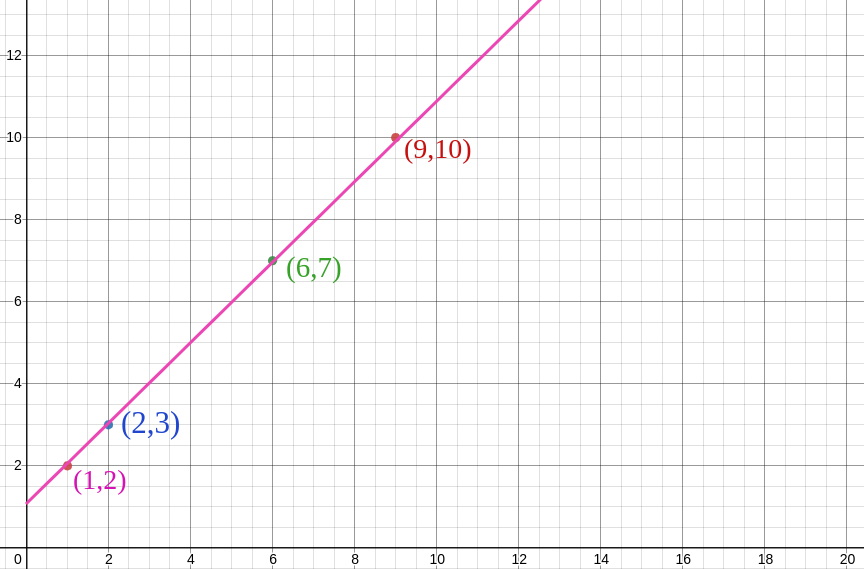
After drawing a line over these points it becomes a function, I hope you remember functions from our blogpost Math as a language.
Candies
Dollars
Reminding about functions, It is similar to tools and applications in your house, you give something and in return you get something.
Like a refrigerator, you give water and it gives out ice.
A microwave, you input corn seeds and you get popcorn.
A blender, you put tomatoes and you get a puree.
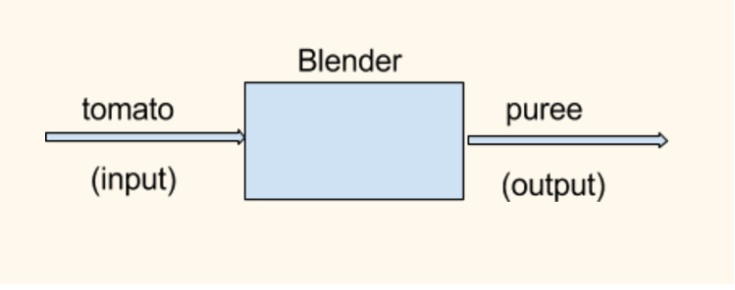
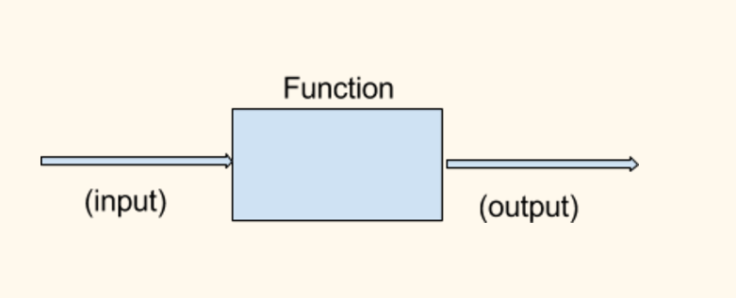
Just like refrigerator, microwave and blender, this pink line on the plane is a function and the input points are the horizontal axis and output points are vertical axis.
So let's test some inputs on our new function, if I had 8$ then how many candies I will have.
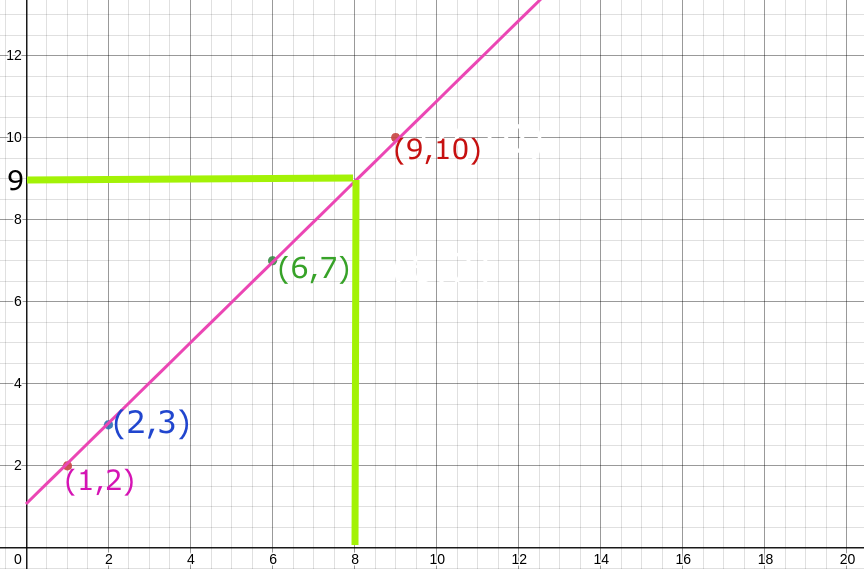
9 candies
Similarly, if I had 5$ then..
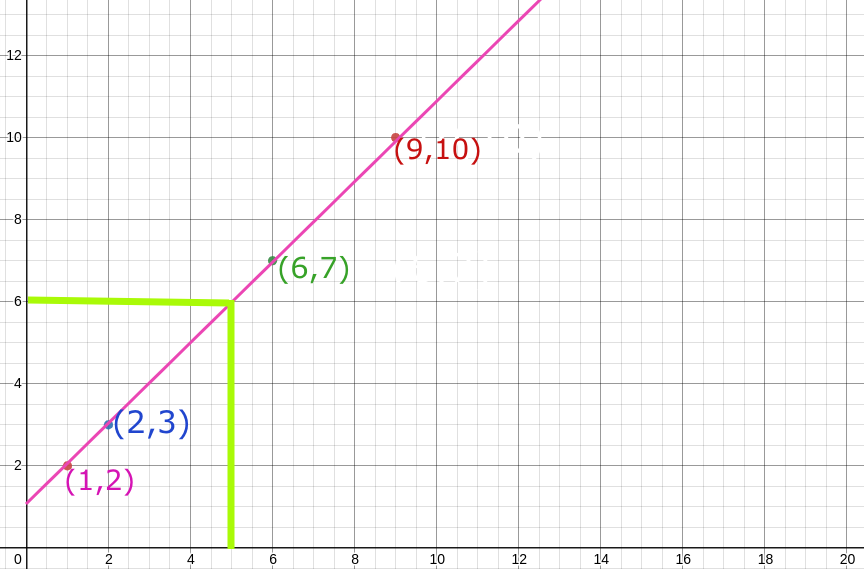
6 candies
Now you have totally understood about a function on a plane, but we don't have all the time in the world and space, so we had to come up with quick and smart, so we came up with algebraic function, which is quick and short. Let's see.
We can literally find a pattern that output is one extra than the input. so
f(x) = x + 1
f(5$) = 5 + 1 = 6 candies
f(8$) = 8 + 1 = 9 candies
Let's look at one more example, to make you clearer.

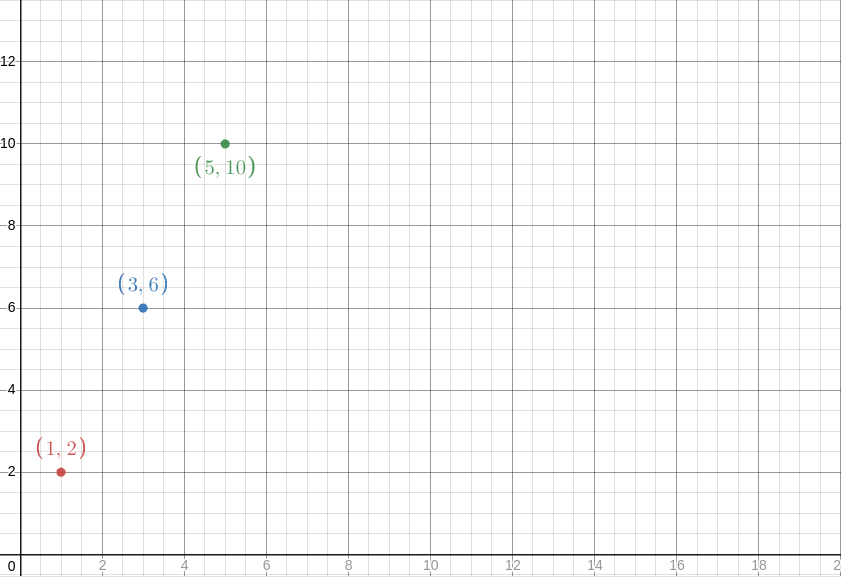
If you buy 1 toothpaste you will get 2 toothbrush for free.
If you buy 4 toothpaste you will get 8 toothbrush for free.
If you buy 7 toothpaste you will get 14 toothbrush for free.
Now on the cartesian plane.
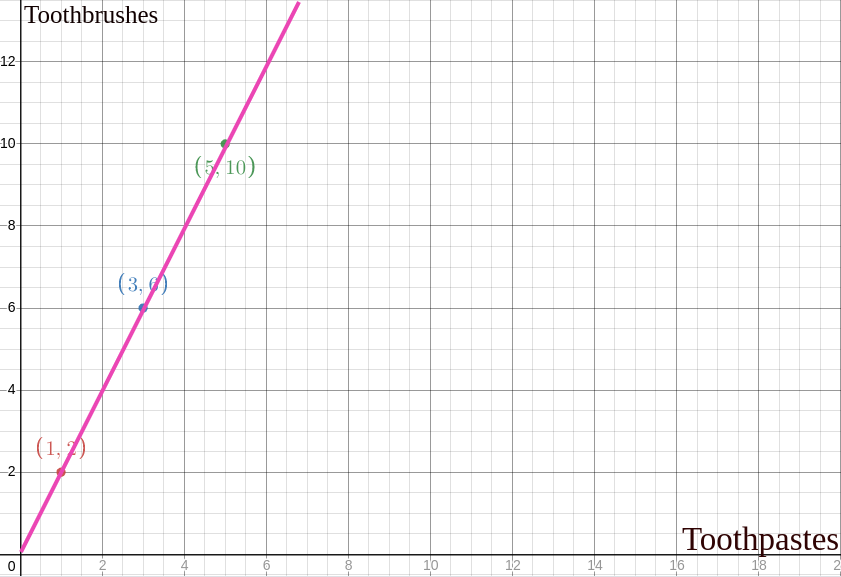
Then with the function in the pink line.
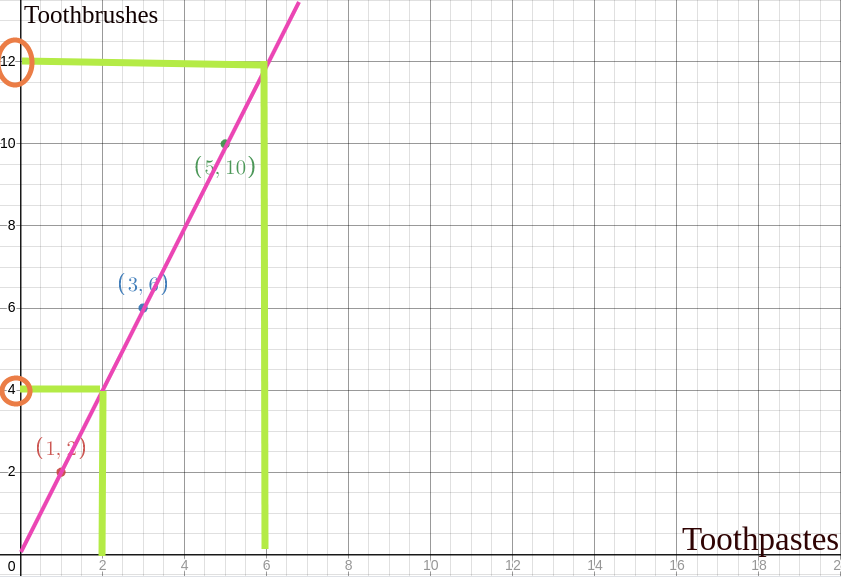
Now testing on newly created function, how many free toothbrushes I will get if I buy 2 and 6 toothpastes.
The algebraic function for this will be
f(x) = 2x + 0
As we can notice from the pattern
or generally
f(x) = 2x
f(2 toothpaste) = 2*2 = 4 toothbrushes
f(6 toothpaste) = 2*6 = 12 toothbrushes
That was fine, let's look at a little trickier example.
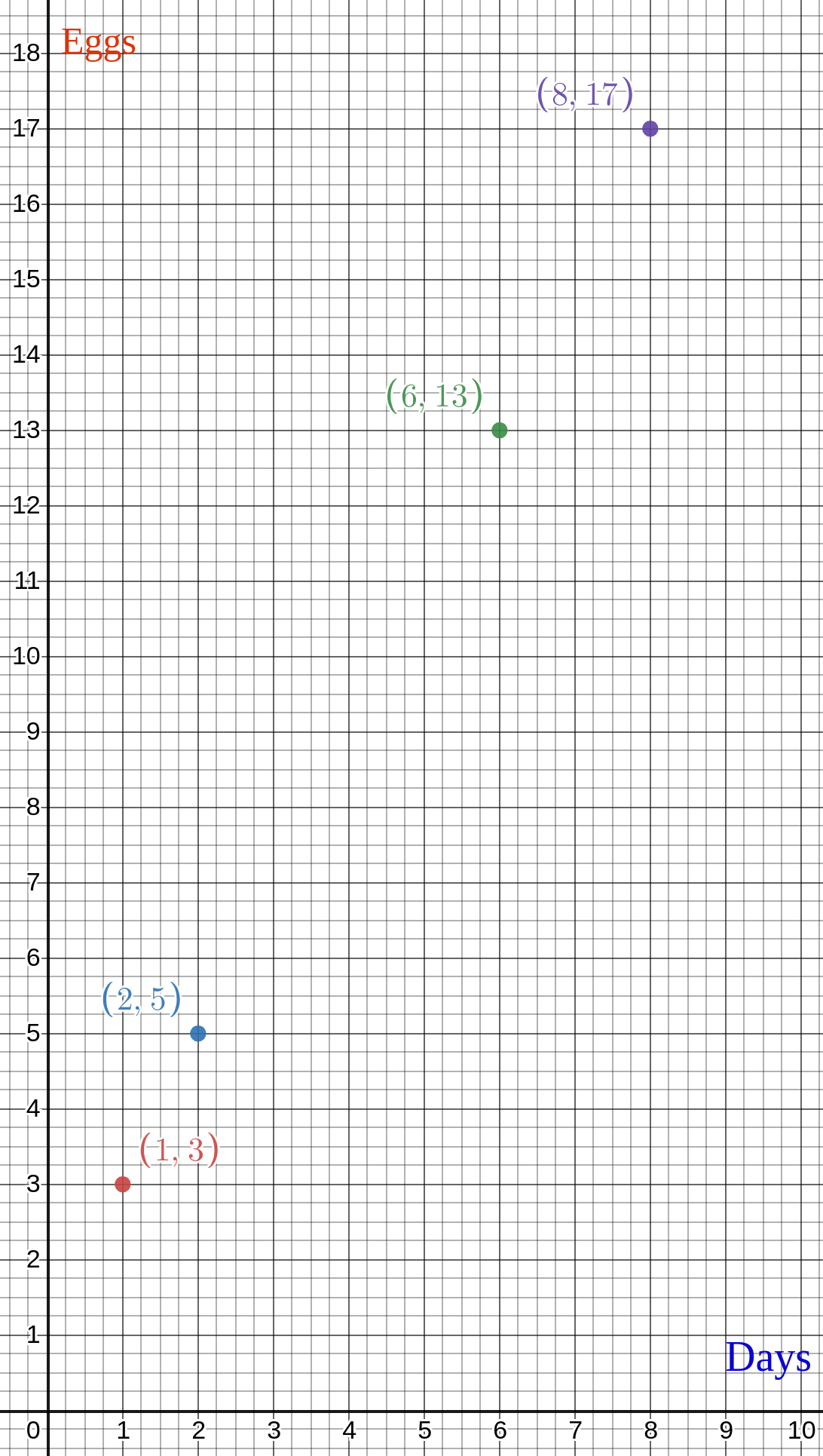
A chicken, in 1 day lays 3 eggs.
In 2 days, it lays 5 eggs.
In 6 days, it lays 13 eggs.
In 8 days, it lays 17 eggs.
so tell me how much the chicken will lay eggs in 4 and 7 days?

Same process, just plot.
And creating a new function with pink line
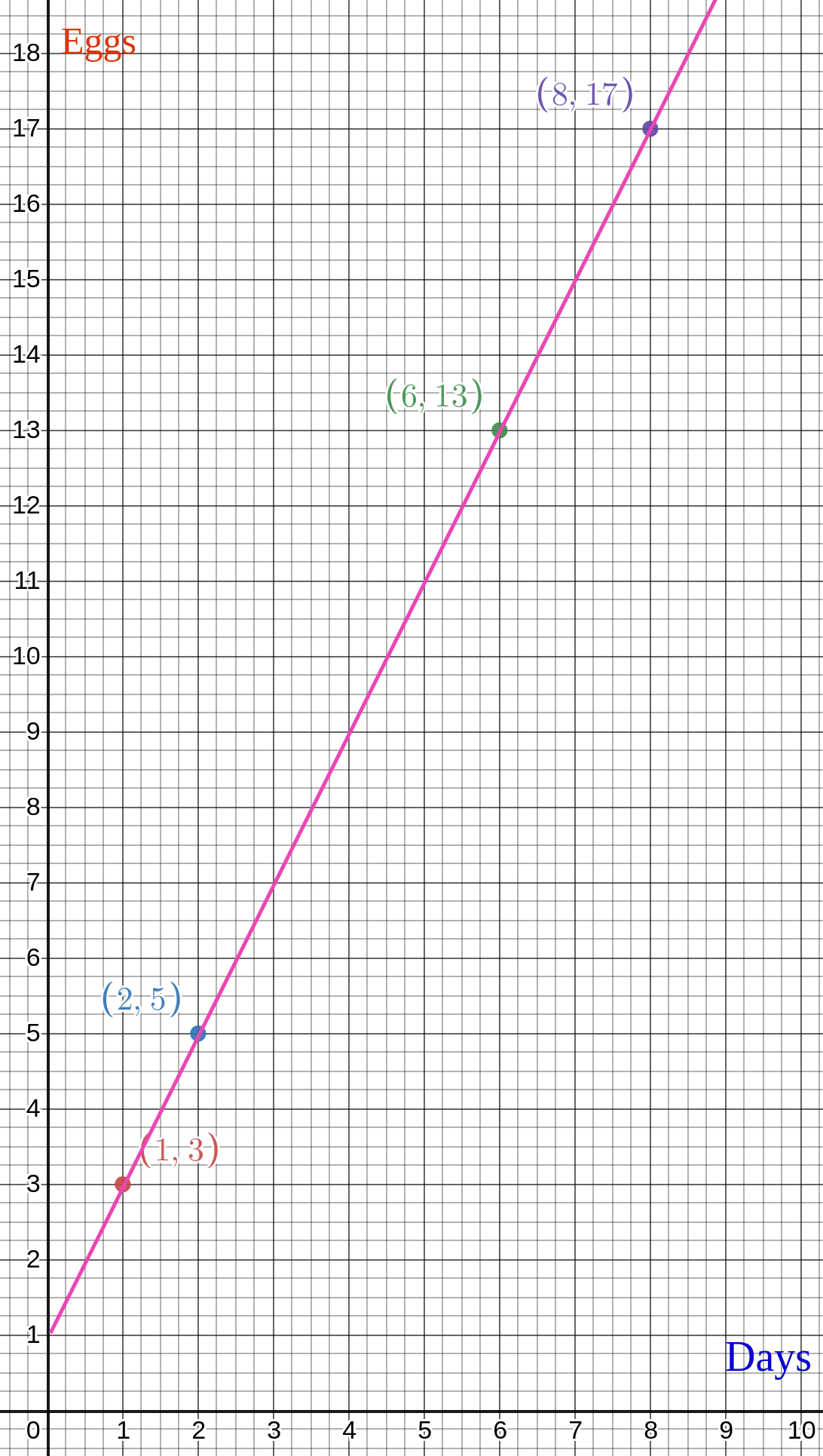
Then predicting for number of eggs in 5 and 7 days
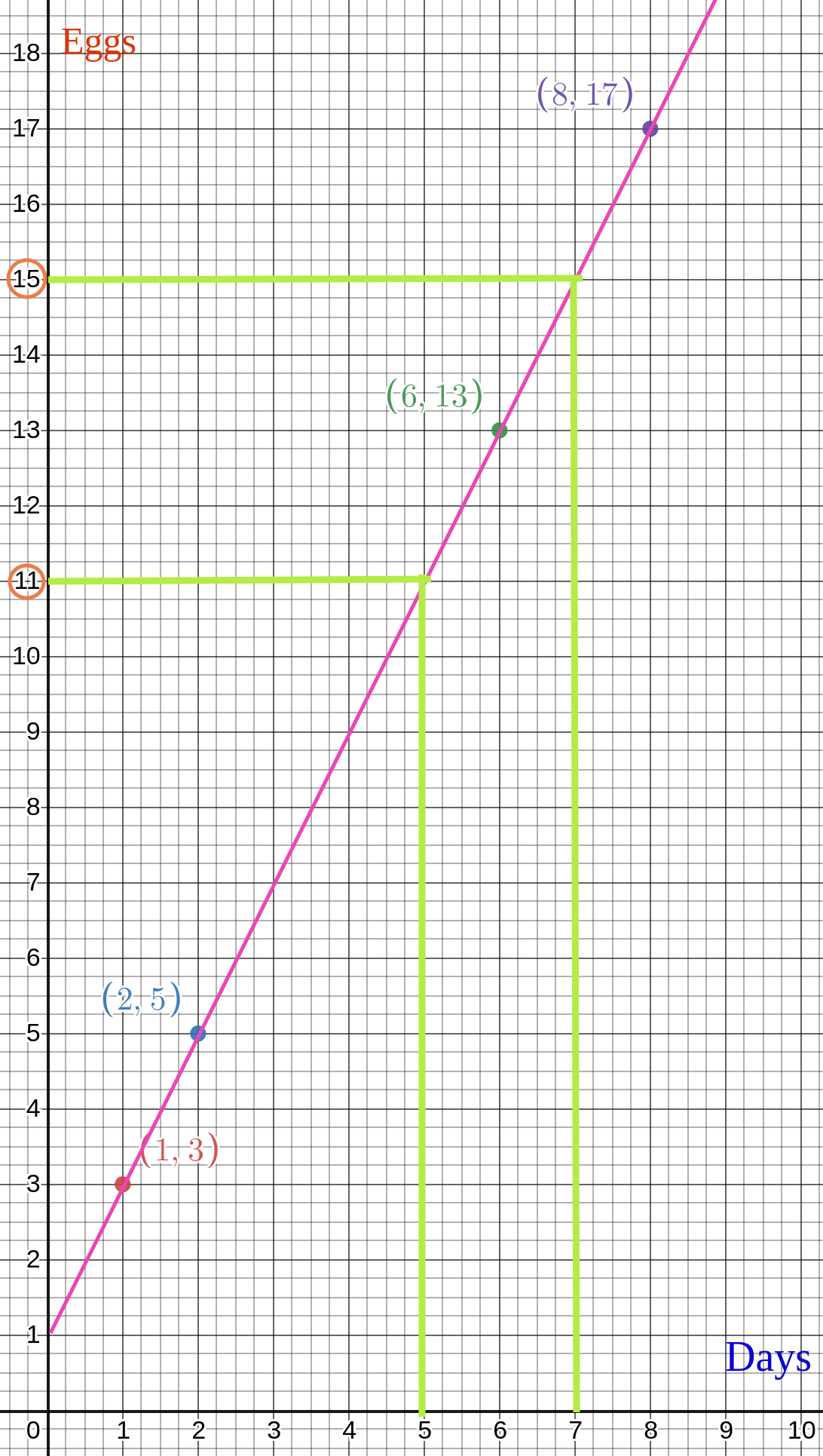
So what will be the algebraic function for this equation?
By looking over so many examples we concluded that by looking at the steepness of the line and the intercept at the vertical axis we can figure out the algebraic function or the equation of the line.
steepness * x + intercept at vertical axis
steepness * x + 1
But you must be wondering what steepness is?
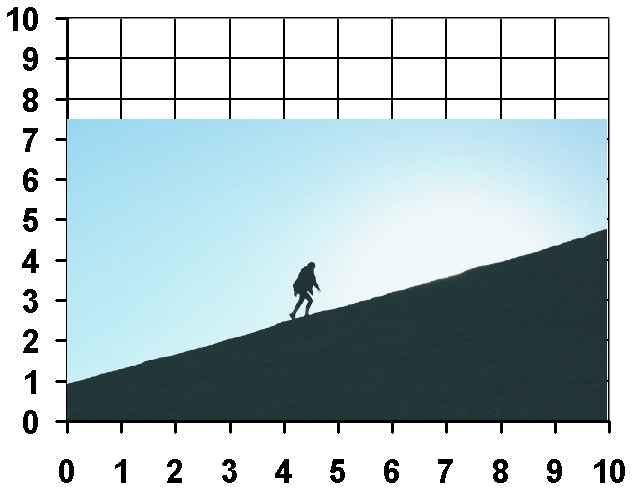
steepness = rise/run = 5-1/10-0 = 4/10 = 0.4
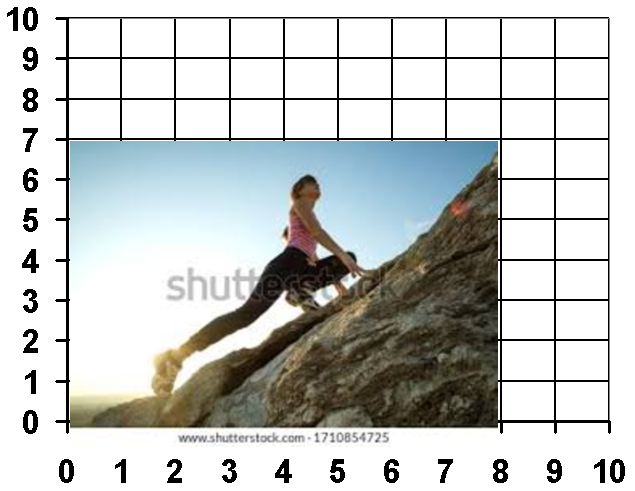
steepness = rise/run = 7-0/8-0 = 7/8 = 0.8

steepness = rise/run = 10-0/4-0 = 10/4 = 2.5

steepness = rise/run = 10-0/8-6 = 10/2 = 5
Now you must have got an idea about the steepness, you can take any two-point in the equation of the line function and take the ratio of how up you travel (height) to how far you traveled (distance) and that will give you steepness or in other words "slope" and also represented by the letter "M".
Now going back to our egg problem,
.png)
steepness * x + intercept at vertical axis
steepness * x + 1
steepness = difference between points in heights/difference between points in distance
steepness = 5-3/2-1 = 2/1 = 2
or
steepness = 13-5/6-2 = 8/4 = 2
or
steepness = 17-13/8-6 = 4/2 = 2
or
steepness = 19-1/9-0 = 18/9 = 2
After inserting the value of steepness in the equation
steepness * x + 1
2 * x + 1
2x + 1
Now the calculating number of eggs in 4 and 7 days with our new algebraic function.
f(x) = 2x + 1
f(4 days) = 2*4 + 1 = 9 eggs
f(7 days) = 2*7 + 1 = 15 eggs
Now I think we have learned enough about functions and coordinate planes, so it's time to solve our initial problem.
person A gives something to person B and in return person B gives something in return, let's see this through a table.
Problem 1.
| Person A | Person B |
|---|---|
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
| 4 | 11 |
| 5 | 13 |
| 6 | 15 |
So how much a person B will give when person A gives 7?
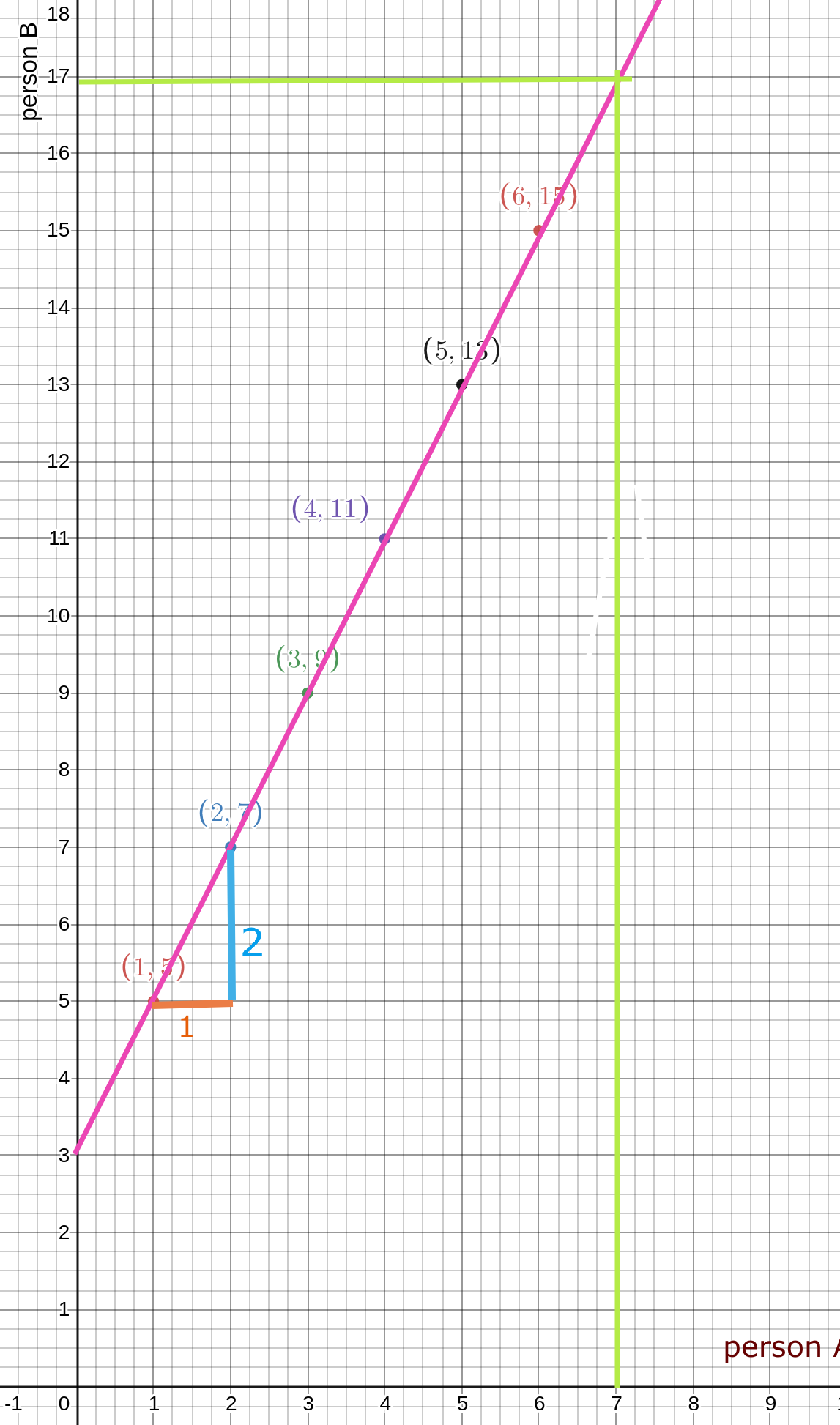
By using the cartesian plane we got our answer that person B will give 17 on given 7. Now let's see the algebraic function for this.
steepness * x + intercept at vertical axis
intercept at vertical axis = 3
steepness = 7-5/2-1 = 2/1 = 2
Putting it all together.
2 * x + 3
Now the calculating how much a person B will give when person A gives 7 with our new algebraic function.
f(x) = 2x + 3
f(7) = 2*7 + 3 = 14 + 3 = 17
If you closely observe this, it is the same reward function to reward kids after exam grades, that we have learned earlier in the previous blog Math as a language