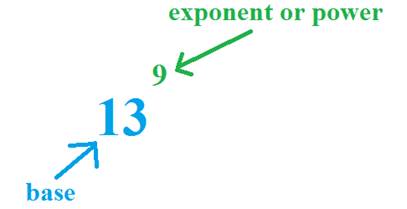Exponents

As we know, repetitive Addition is known as Multiplication. Similarly, repetitive Multiplication is known as Exponents or Powers.

2 + 2 + 2 = 2 x 3
2 x 2 x 2 = 2 ^ 3

or

2 x 2 x 2 = 2³

Repetition of 3's are called Cube, like above in the example.

And the repetition of 2's are called Square like 2 x 2 i.e 2².

These were exponents but this is not the end, real problems come when you have to multiply and divide a large number of exponents and it could become really lengthy and there we have to act smart. Like these ones:

2³¹ / 2²⁹

Next will be to solve 2³¹ by multiplying 2 repeatedly till 31 times like this 2 x 2 x 2 ........2, similarly with 2²⁹.

2147483648 / 536870912

After dividing

2147483648 / 536870912

Dividing this will be a daunting task to do.

After division it will be 4

Deduction and Prototypings

Using this technique, we could really find a pattern to solve a complex math problem by just using small numbers which eases up the calculation, and finding a pattern becomes easier then, Let's see in our case.

2³¹ / 2²⁹

Instead

2³ / 2²

2 x 2 x 2 / 2 x 2

8 / 4

2

Now solving this without simplifying exponents.

2³ / 2²

and you know division means repetitive subtraction so,

2^3-2

2¹

2

As we can see, the above solution is pretty simple and we can see the pattern that when the base is the same we can literally subtract exponents for division and we will get the same answer 2.

And now applying the same observation to our main problem with the bigger numbers.

2³¹ / 2²⁹

2^31-29

2²

4

Aha! That was easy right far less calculation and no big numbers and yet we still got the same answer 4.

So we conclude for our practice that,
while dividing these kind of number we subtract powers with the same base.

Similarly

while multiplying these kind of number we add powers with the same base. Try a example by yourself and test that.

Zero Power Rule

Any number with power 1 is always the number itself. As we know only one repetition of anything will the number itself

2¹ = 2

or

3¹ = 3

So have you ever thought that what will be the answer to any number with power 0?

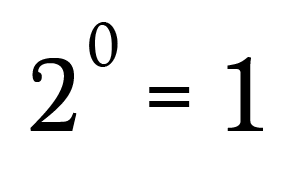
Yes! it will be 1 only either the number be 2, 3 or any number.

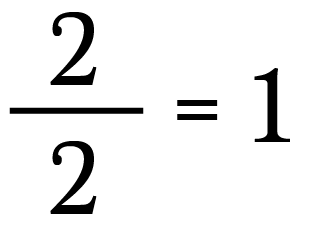
As we know how many groups of 2 can be made into 2 things i.e only one group.

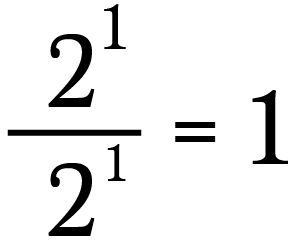
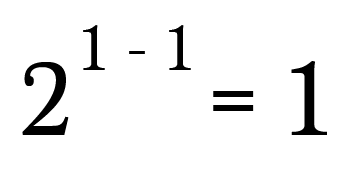
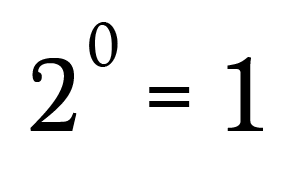
Negative exponents

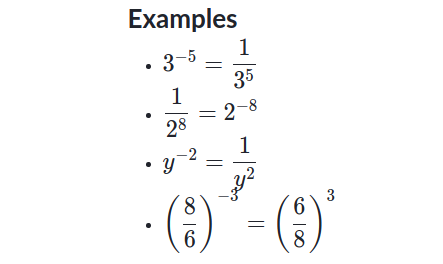
So why do we define negative exponents this way? Here are a couple of justifications:

And we can also use our previous deduction to justify this.

Similarly, we can use our deduction and prototyping to explore more about exponents.