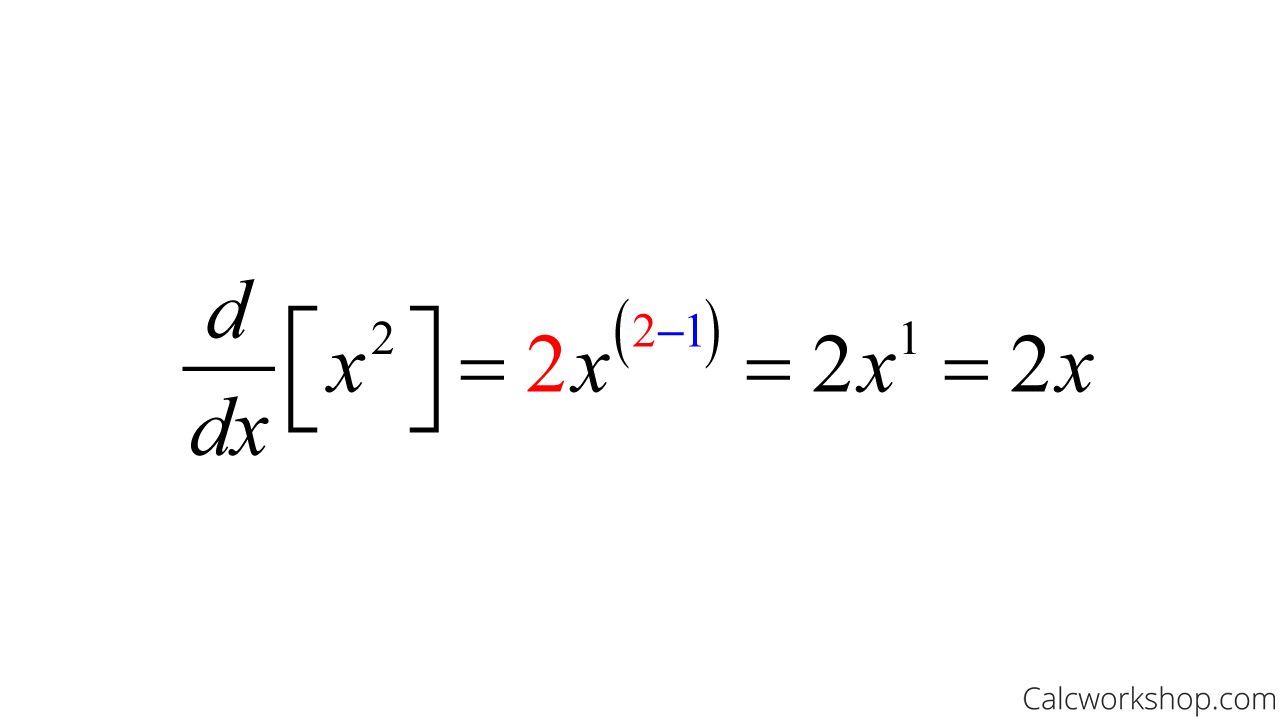A car 🏎 started and reached 1 meter in 1 sec and 4 meters in 2 sec and 9 meters in 3 sec and so on, like the distance traveled was square of the time taken.
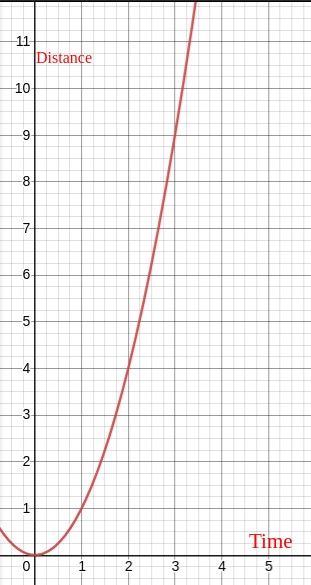
And after plotting Time in sec on the horizontal axis and Distance in meters on the vertical axis, we could clearly see that it's a function of X2.
Now if I ask you to tell the speed(velocity) in which the car traveled till 12 meters.
Distance = Speed x Time
Speed = Distance/Time
Speed = 12meters/3.5sec
Speed = 3.4 meters/sec
This means the car traveled 3.4 meters per second all the time to reach 12 meters but this is not true at all, as we know no object can start moving at a certain speed it has to start from 0.
So we can conclude that the above speed(velocity) is not the exact or instant speed but it's more like an average speed throughout the journey.
To get the instant speed, we break down the time of the journey in small intervals to get the instant speed at that small time period. Like from 0 to 1, 1 to 2, 2 to 3 and so on.
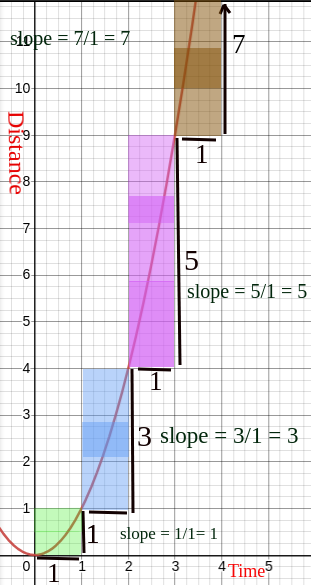
And we calculated the speed of those time periods using the slope of that time periods, as both are the same in this case.
$slope=\frac{difference\hspace{0.1cm}in\hspace{0.1cm}vertical\hspace{0.1cm}axis}{difference\hspace{0.1cm}in\hspace{0.1cm}horizontal\hspace{0.1cm}axis} = \frac{difference\hspace{0.1cm}in\hspace{0.1cm}distance}{difference\hspace{0.1cm}in\hspace{0.1cm}time}= speed$
As we can see speed is 1 meter per sec between 0 to 1 sec and from 1 to 2 sec speed is 3 meters per sec and so on..
But this is completely not accurate as I will tell you next.
.png)
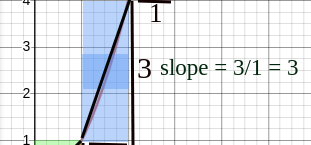
If you see this green area, there are two line functions, very close, very similar to each other. The red one is our function X2 and the black one is the nearest straight line function which I have drawn and the speed which we have calculated using slope is taken from the black line function because the slope is consistent(i.e 1 m/sec) even if you break that function into two or three.

Whereas, if you draw this approximately equal black straight-lines function alongside these two smaller parts, you will find two different slopes i.e 0.5 m/sec, and 3 m/sec which is far more accurate than the combined `1 m/sec.

So we can conclude that the straight-line approximation function we created to calculate slope/speed of our function at those time intervals fits better as we go small and small intervals and give accurate results instead of loosely fitting approximation like one in the previous one from 0 to 1.
Similarly, slope 3 between the time period 1 to 2 sec is not accurate as the approximation function doesn't fit as well as it will fit when break the time period into two, 1 to 1.5 sec and 1.5 to 2 sec.
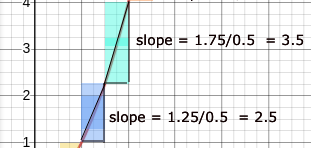
And again now calculating slope/speed but this time with a much smaller time period from 0 to 0.5, 0 to 1, 1 to 1.5, and so on, using our same approximation method.
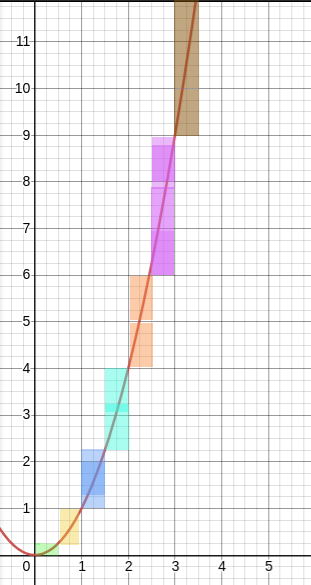
This time we can say that the speed we calculated at every instant of the journey is quite accurate by seeing the fitting line below and the more the smaller time period greater the accuracy.
.png)
And if you think wisely, longer the time span to calculate the speed more the variable speed it will encompass and shorter the time span more constant and instant speed you will get like you are riding a bike and it is a high chance that you will change the speed within a minute but within a second you can't do much so automatically you will get instant and accurate speed at that time.
Now lets plot our results
- Average speed 3.4 m/s
Instant speeds within a time interval of 1 sec which are 1, 3, 5, 7 metres per sec and so on.
Instant speeds within a time interval of 0.5 sec which are 0.5, 3, 2.5, 3.5, 4, 6, 6 metres per sec and so on.
Similarly, We calculated slope/speeds at even a small time interval than previously i.e 0.2 sec and plotted in Time vs Speed plot.
Similarly, We calculated slope/speeds at even a small time interval than previously i.e 0.2 sec and plotted in Time vs Speed plot.
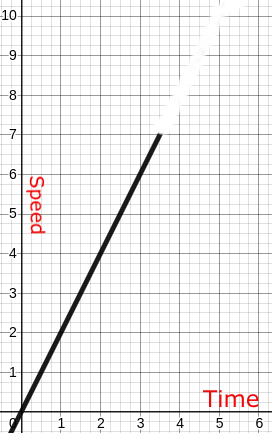
And if you take a closer look at this graph, you will see that at 1 sec speed is 2 m/s, at 2 sec the speed is 4 m/s and at 3 sec the speed is 6 m/s and so on. So we can say that the following newly created function is 2X.
.png)
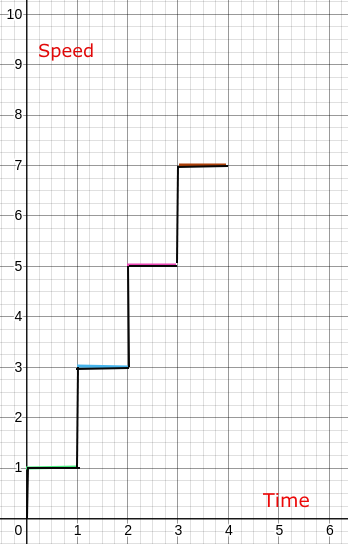
.png)
.png)
.png)
In the end, we can conclude that If we break a function into so many tiny parts that so that its straight line approximation function fits well with it and hence we can calculate accurate slopes and in this case its speed and once we assemble these we can get the slope/speed of the whole function.
In this example, we got the slope/speed of the X2 function equal to 2X.
Differentiation is the difference in speeds throughout the function, and speed is the rate of change, how quickly it's changing or how slowly it's changing.
In Math language we can say our function to know the distance covered by the car with respect to time is Y = X2, where x is the Time and y is distance.
$Y = X^2$
The Slope of Y with respect to time = X2.
The Speed of Y with respect to time = X2.
The Differentiation of Y with respect to time = 2X. where differentiation is known letter small "d".
$\frac{dY}{dTime} = \frac{dX^2}{dTime}$
$\frac{dY}{dTime} = 2X$